Направления исследований.

Основные направления исследований связаны с решением нестационарных задач в системах с неоднородностями различной природы:

Системы с подвижными нагрузками.

• Нестационарные задачи механики фазовых превращений.

• Нестационарные процессы в системах с локализованными модами колебаний.

Основные результаты:

• Решены нестационарные динамические задачи о возникновении зародыша новой фазы в упругом стержне вследствие столкновения двух волн [⤤].

• Предложено объяснение классического парадокса Стокса в задаче об инерционной подвижной нагрузке [⤤].

• Получены аналитические решения, описывающие нестационарные движения в системах с локализованными модами колебаний и медленно меняющимися во времени параметрами [⤤], [⤤], [⤤].

• Получено решение, описывающее переход через резонанс в системе с локализованной модой [⤤].

• Получено аналитическое решение задачи, описывающее нестационарные колебания в системе «струна на винклеровском основании — подвижной осциллятор» при ускоренном движении осциллятора [⤤].

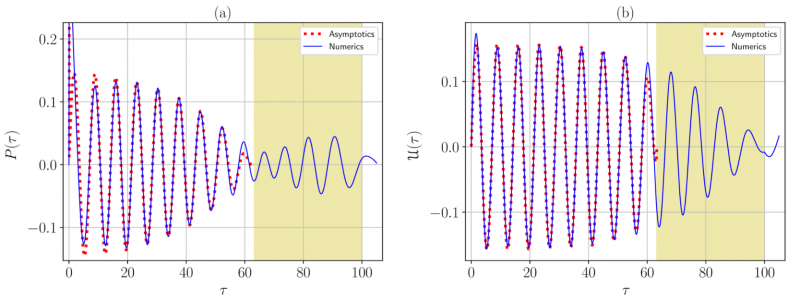
Сравнение асимптотического и численного решений для ускоренно движущегося осциллятора. (a) Внутренняя сила, (b) перемещение.