Направления исследований:

Изучение нестационарных задач со свободными границами, описывающих в рамках модели Навье–Стокса эволюцию двух вязких несмешивающихся жидкостей с неизвестной поверхностью раздела, на которой учитывается поверхностное натяжение. Исследование глобальной однозначной разрешимости в пространствах Соболева–Слободецкого и Гёльдера, нахождение оценок решений, исследование вопроса об устойчивости движения с течением времени.

Основные результаты:

Получена общая картина гладкости решений задач, описывающих одновременное движение двух вязких жидкостей. В частности, проведено исследование разрешимости в пространствах Соболева–Слободецкого и Гёльдера начально-краевых задач для уравнений Стокса и Навье–Стокса с замкнутой границей раздела двух сред. Оценки решения задачи о движении двухфазной несжимаемой капиллярной жидкости в ограниченной области при малых начальных данных являются точными и гарантируют устойчивость решения с течением времени.

Результаты опубликованы в монографии И. В. Денисова, В. А. Солонников «Движение капли в несжимаемой жидкости», Санкт-Петербург: Лань, 2020, 296 с. [⤤] (перевод: I. V. Denisova, V. A. Solonnikov, “Motion of a Drop in an Incompressible Fluid”, Springer, 2021, 316 с. [⤤]).

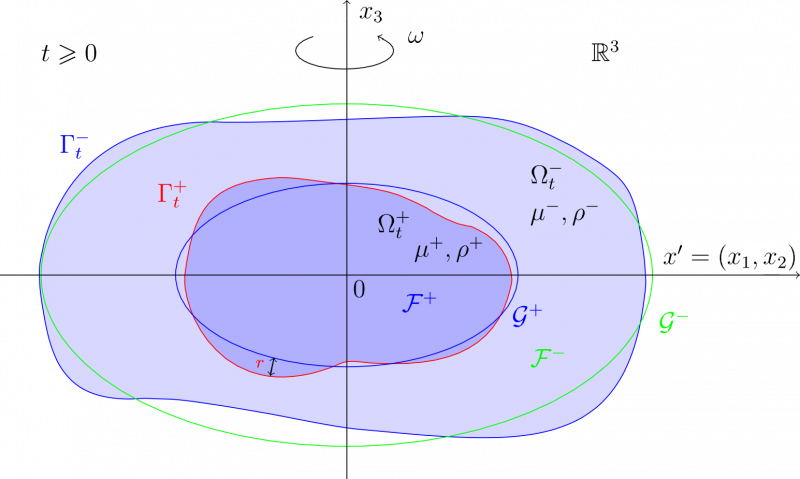
Изучается проблема устойчивости равномерно вращающейся капли, состоящей из двухслойной вязкой самогравитирующей капиллярной жидкости. Для этой задачи получена глобальная однозначная разрешимость при малости начальных данных, внешних сил и скорости вращения, а также близости заданных начальных поверхностей к некоторым осесимметричным фигурам равновесия. Доказано, что если вторая вариация функционала энергии положительна, то малое возмущение аксиальносимметричной двухфазной фигуры равновесия экспоненциально стремится к нулю, а движение капли с течением времени переходит во вращение жидкой массы как твёрдого тела [⤤].