Волны на поверхности жидкости представляют собой широко распространенное физическое явление; математические задачи теории волн возникают в связи с важными практическими приложениями (прежде всего, расчетом гидродинамических нагрузок на погруженные тела). Изучаются задачи, описывающие в линейном приближении установившееся движение идеальной, тяжелой жидкости со свободной поверхностью в присутствии препятствий. Отыскание однозначно разрешимых постановок задач является одним из ключевых вопросов [⤤], зачастую требующим развития оригинальных математических методов; например, рассмотрение локализованных мод часто сводится к изучению точечных собственных значений на непрерывном спектре.

Основные результаты:

• Найдены условия единственности и разрешимости ряда задач, среди которых плоская задача о потоке жидкости над выступом дна [⤤], задача о поступательном движении тел в однородной [⤤] и двухслойной жидкости [⤤], задача о гармонических по времени колебаниях жидкости в присутствии фиксированных тел [⤤], [⤤] и препятствий [⤤], в том числе с учетом поверхностного натяжения [⤤], а также свободно плавающих тел [⤤], [⤤], [⤤].

• Изучен вопрос о дополнительных условиях, превращающих задачу Неймана–Кельвина в однозначно разрешимую, для тел, либо пересекающих свободную поверхность, либо поверхность раздела двух слоев разной плотности [⤤], [⤤], [⤤].

• Для задачи о поступательном движении тел и задачи о колебаниях жидкости в присутствии тел найдены критерии однозначной разрешимости. Разработаны численные алгоритмы и впервые обнаружены примеры неединственности с полностью погруженными телами [⤤], [⤤], [⤤], [⤤], [⤤], [⤤] (в том числе с учетом поверхностного натяжения и в двухслойной жидкости). Показана связь примеров неединственности с аномально большими значениями волнового сопротивления. На рисунке показано тело, для которого существует пример неединственности, и картина линий тока [⤤].

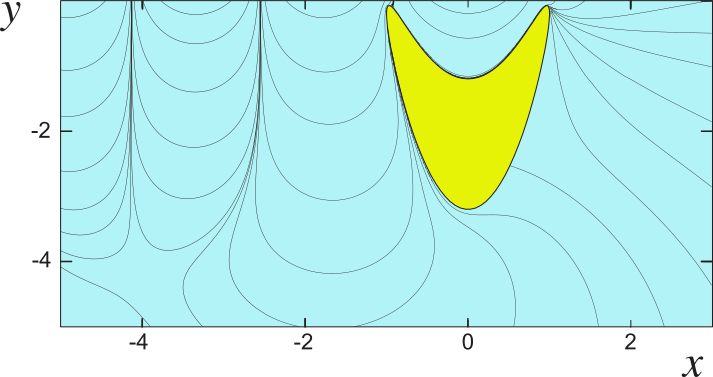
• Получен ряд примеров неединственности для тел, частично погруженных в жидкость или пересекающих интерфейс. Использована обратная процедура: для заданного потенциала скоростей разыскивается геометрия, для которой он является решением однородной задачи [⤤], [⤤]. Существенный прогресс был достигнут в задачах о совместных колебаниях жидкости и свободно плавающих тел [⤤], [⤤] и [⤤]. В построенных примерах локализации мод [⤤] погруженная часть тел осесимметрична, а тела неподвижны, хотя и плавают свободно, — на рисунке показан пример такой структуры.

• Рассмотрена задача о колебаниях жидкости в присутствии частично погруженных тел в случае, когда жидкость ограничена сверху плавающей ледяной шугой. Установлено существование локализованных мод колебаний и построены примеры тел, поддерживающих такие моды с конечной энергией. С другой стороны, удалось найти условия отсутствия локализованных мод [⤤], [⤤].

• Рассмотрены задачи о поступательном движении тел и о колебаниях тел в двухслойной жидкости. При этом важной особенностью является более сложная картина гидродинамических нагрузок в связи с наличием внутренних волн, связанных с явлением «мертвой воды». Изучены вопросы однозначной разрешимости, найдены примеры неединственности, исследованы свойства решений, включая гидродинамические нагрузки и их возможные особенности: см. [⤤], [⤤], [⤤], [⤤], [⤤] (задача о движении), [⤤], [⤤], [⤤] (задача о колебаниях).

• Для трехмерной задачи о движении тел в жидкости со свободной поверхностью (задача о корабельных волнах) разработаны алгоритмы быстрого вычисления функции Грина и производных. С этой целью развиты методы вычисления интегралов от быстро и негармонически осциллирующих функций по полубесконечному интервалу [⤤].

• Изучены собственные моды колебаний жидкости со свободной поверхностью в вертикальных круговых и кольцевых цилиндрических контейнерах. Анализировался эффект нарушения осевой симметрии из-за наличия радиальных перегородок, идущих вертикально от свободной поверхности к дну. Показано, что наличие перегородки приводит к существенному изменению свойств собственных значений и собственных функций [⤤].