Нагруженные упругие оболочки активно исследуются в связи с богатыми приложениями в технике и строительстве. Это один из важнейших элементов при моделировании акустических волноводов, различных трубопроводов, опор морских буровых установок и других гидротехнических сооружений. Волны, распространяющиеся в подобного типа системах, вызывают колебания и вибрации как самих оболочек, так и их сочленений, что может влиять на прочностные свойства всей системы. Наличие разного рода нагрузок значительно усложняет характер волновых процессов. В качестве таких нагрузок может выступать среда, окружающая оболочку или находящаяся внутри оболочки жидкость. А также различные локальные нагрузки, например ребра жесткости на оболочке, массивные элементы на ней и т.д. Все это требует исследования не только классических, но и более сложных моделей оболочки, что вызвано, в частности, актуальностью проблемы водородного охрупчивания нефтегазопроводов. Водородное воздействие приводит к ослаблению материала конструкции, которое существующими нормами расчета не учитывается, что может привести к авариям. Указанные технические проблемы требуют прогнозирования поведения оболочки и возможности возникновения таких режимов, а также вывода формул для восстановления параметров оболочки по экспериментальным данным.

Направления исследований:

• Гранично-контактные задачи (ГКЗ) математической акустики. Точные, асимптотические и численные решения ГКЗ (в том числе для систем оболочка – среда)

• Исследование потоков энергии в системах оболочка – среда.

• Периодически нагруженные оболочки.

• Неоднородные оболочки, в том числе ослабленные водородом.

Основные результаты:

• Предложена постановка ГКЗ взаимодействия среды и оболочек типа Тимошенко и Кирхгофа – Лява на основе моделей оболочек В.В.Елисеева. Получены, согласованные с законом сохранения энергии в системе, выражения для потоков энергии, в криволинейной системе координат, в системах оболочка – среда. [⤤]

• Получены точные аналитические решения и предложены упрощенные модели для ряда гранично – контактных задач математической акустики с гармонической зависимостью от времени. В частности, для свободных колебаний погруженных в жидкий волновод мембран, пластин, цилиндрических оболочек, а также концентрических цилиндрических оболочек, частично заполненных жидкостью и окруженных средой. [⤤], [⤤], [⤤]

• Найдено точное аналитическое представление функции Грина задачи о гармонических колебаниях цилиндрической оболочки, частично погруженной в жидкость. Что позволяет рассчитывать вынужденные колебания цилиндрической оболочки под действием сил, действующих как в подводной, так и в надводной части оболочки, а также на уровне жидкости (например, влияние льда). [⤤]

• Проведен анализ структуры, как потоков энергии, так и кинематических и динамических характеристик вибрационного поля в системе оболочка – среда, в окрестности особых точек дисперсионных кривых. Найдена асимптотика потоков энергии. В частности, исследована перестройка компонент потоков энергии в окрестности точек виринга для оболочек типа Кирхгофа – Лява, как “сухих”, так и нагруженных средой. Показана эффективность использования потоков энергии, поскольку учитываются не только кинематические и динамические характеристики вибрационного поля, но и сдвиг фазы между ними. Это позволяет прогнозировать опасные режимы колебаний оболочек и систем оболочка – среда при их проектировании. [⤤], [⤤], [⤤]

• Обнаружен эффект отрицательной групповой скорости для “сухих” оболочек типа Кирхгофа – Лява. Этот эффект исследован как для “сухих” оболочек, так и для оболочек нагруженных жидкостью или Винклеровским основанием. Получены асимптотические оценки диапазонов частот и волновых чисел, где наблюдается эффект с отрицательной групповой скоростью, а также оценки максимальной отрицательной групповой скорости в системе. Эти результаты могут быть полезны для прогноза возникновения опасных режимов работы трубопроводов и других подобных систем. [⤤], [⤤], [⤤], [⤤]

• Обнаружен эффект факторизации уравнений границ полос пропускания и запирания в бесконечных периодических оболочках. Получены явные выражения факторизации этих уравнений в случае стержней и балок, нагруженных периодическими массами. Исследованы потоки энергии и вибрационные поля в такого рода системах. [⤤], [⤤], [⤤]

• Получены формулы, связывающие сдвиг частоты, вызванный водородным охрупчиванием оболочки, с параметрами оболочки, коэффициентами затухания и степенью износа со временем. Это, в свою очередь, позволяет прогнозировать сдвиг частот и, тем самым, избежать нежелательного выхода оболочки на опасный для ее прочности режим смены характера колебаний. [⤤], [⤤]

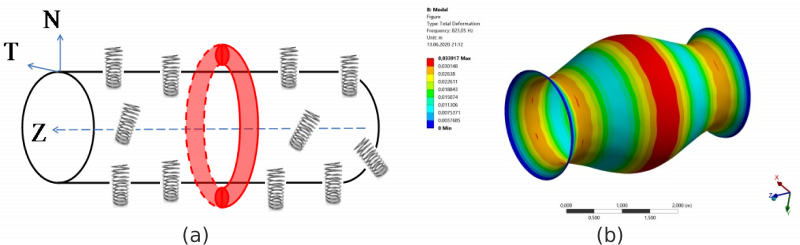
Колебания цилиндрической оболочки на Винклеровском основании, нагруженной массовым пояском: (a) физическая модель, (b) визуализация смещений