A plane nonlinear problem with a free boundary is studied, which describes steady waves on the surface of an ideal, incompressible fluid of finite depth, taking into account the vortex nature of its motion. In the case of a solitary wave, the flow has the following properties: at both infinities it is a unidirectional, shear, supercritical flow of constant depth, the latter corresponding to the given Bernoulli constant of the original problem. This mathematical model of waves under the action of gravity is important for taking into account the vorticity of a given type in the interaction of waves with currents; It follows from observations that this behavior is very common in nature.

Main results:

1. Two integro-differential equations of the Babenko type are derived and investigated to describe bifurcations, as a result of which nonlinear Stokes waves arise on the surface of a horizontal irrotational flow of finite depth, and as a result of branching of the bifurcation curves, these waves change their profile. For the first time, the corresponding diagrams, including those with multiple branching, were obtained numerically, and wave profiles were found for each of the branches, including extreme-shaped waves with corner points on crests. See publications: [⤤] and [⤤].

2. The existence of a new type of solitary waves on the flow surface with constant negative vorticity, the main feature of which is the presence of a stagnation point (stagnation) inside the vorticity region of the Kelvin "cat's eye" type, is proved. This bottom eddy is symmetrical with respect to the vertical passing through the wave crest. The considered type of fluid motion is observed in nature. See publications: [⤤] and [⤤].

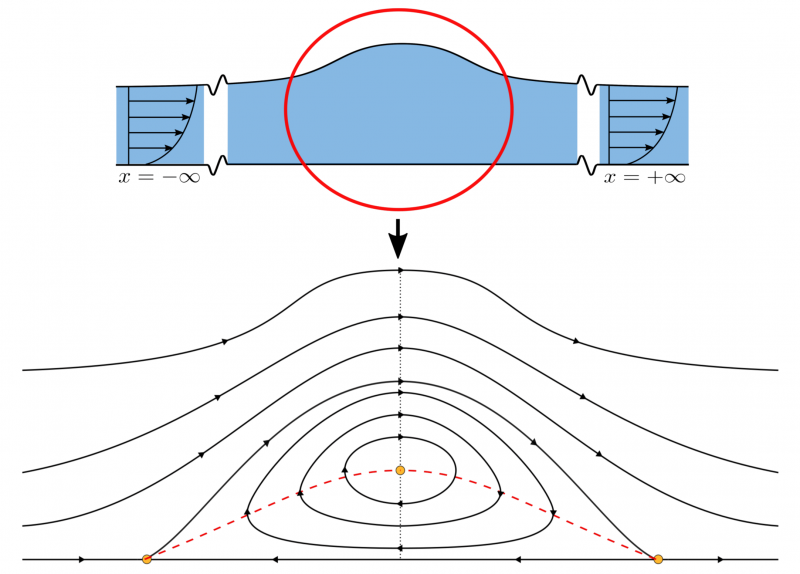
Illustration of cat's-eye vorticity streamlines.

An interesting phenomenon predicted within the framework of the model is the presence of countercurrents, which are separated from one another by the so-called critical layers, and the latter are characterized by the presence of stagnation points. It is shown that the counterflow necessarily takes place in the case when the minimum of the wave profile exceeds a certain critical value. In addition, a constraint on the admissible values of the Bernoulli constant is found. New boundaries are found for the maxima and minima of wave profiles, which are valid for all their types, including bulbous waves, for which stationary propagation is possible instead of breaking.