Direction of research:

A study of non-stationary problems with free boundaries, governing the evolution of two viscous immiscible liquids with an unknown interface, on which surface tension is taken into account, in the framework of the Navier-Stokes model. Investigation of global unique solvability of the problems in the Sobolev–Slobodetskiǐ and Hölder spaces, a priori estimates of solutions, a study of motion stability over time.

Main results:

A general picture of the smoothness of solutions to the problems on the simultaneous motion of two viscous fluids was obtained. In particular, a study was made of the unique solvability in the Sobolev–Slobodetskiǐ and Hölder spaces of initial-boundary value problems for the Stokes and Navier–Stokes equations with a closed interface between two media. Exponential estimates of the solution to the problem governing the motion of a two-phase incompressible capillary fluid in a bounded domain for small initial data are exact and guarantee the stability of the solution over time. The results were published in the monograph by I. V. Denisova and V. A. Solonnikov, “Motion of a Drop in an Incompressible Fluid”, St. Petersburg: Lan', 2020, 296 p. [⤤] (translation: I. V. Denisova, V. A. Solonnikov, “Motion of a Drop in an Incompressible Fluid”, Springer, 2021, 316 с. [⤤]).

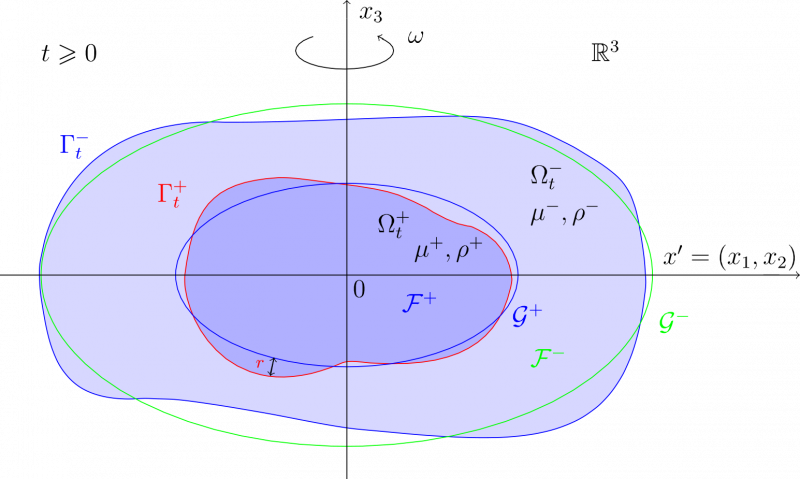
The stability of a uniformly rotating drop consisting of a two-layer viscous self-gravitating capillary liquid is studied. This motion is governed by an interface problem, a global unique solvability of which is obtained for small initial data, external forces and rotation speed, initial surfaces being given close to axisymmetric equilibrium figures. It is proved that if the second variation of energy functional is positive, then a small perturbation of the axially symmetric two-phase equilibrium figure exponentially tends to zero, and the motion of the drop passes over time into the rotation of the liquid mass as a solid body[⤤].