Wave processes in a loaded elastic shell are investigated. Such shells are actively investigated due to rich applications in engineering and construction. This is one of the most important elements in the modeling of acoustic waveguides, various pipelines, supports of offshore drilling rigs and other hydraulic structures. Waves propagating in this type of systems cause oscillations and vibrations of both the shells themselves and their joints, which may affect the strength properties of the entire system. The presence of different kinds of loads significantly complicates the nature of wave processes. These loads may be the environment surrounding the shell or the liquid inside the shell. As well as various local loads, such as stiffening ribs on the shell, massive elements on the shell, etc. All this requires research not only classical, but also more complex models of the shell, which is caused, in particular, by the relevance of the problem of hydrogen embrittlement of oil and gas pipelines. Hydrogen impact leads to weakening of the structural material, which is not taken into account by the existing calculation norms, which can lead to accidents. The mentioned technical problems require prediction of the shell behavior and possibility of occurrence of such modes, as well as derivation of formulas for reconstruction of the shell parameters according to the experimental data.

Areas of research:

• Boundary Contact Problems (BCP) of mathematical acoustics. Exact, asymptotic and numerical solutions of BCP (including shell-media systems)

• Study of energy fluxes in the shell-media systems.

• Periodically loaded shells

• Inhomogeneous shells, including those weakened by hydrogen

Main results:

• The BCP of interaction of the medium and shells of Timoshenko and Kirchhoff–Love type based on V.V. Eliseev shell models are proposed. The invariant expressions for energy fluxes in the shell-medium systems, consistent with the law of energy conservation in the system, are obtained. [⤤]

• Exact analytical solutions have been obtained and simplified models have been proposed for a number of boundary-contact problems of mathematical acoustics with harmonic dependence on time. In particular, for free vibrations of membranes, plates, cylindrical shells, as well as concentric cylindrical shells partially filled with liquid and surrounded by a medium, immersed in a liquid waveguide. [⤤], [⤤], [⤤]

• The exact analytical representation of the Green's function for the problem of harmonic vibrations of a cylindrical shell partially immersed in a liquid has been found. This allows us to calculate the forced vibrations of a cylindrical shell under the action of forces acting both in the underwater and above-water part of the shell, as well as at the liquid level (for example, the effect of ice). [⤤]

• The analysis of the structure of both energy flows and kinematic and dynamic characteristics of the vibration field in the shell-environment system in the vicinity of the special points of the dispersion curves has been carried out. The asymptotics of the energy flows were found. In particular, the rearrangement of the energy flux components in the vicinity of the viring points for the Kirchhoff–Love type shells, both "dry" and loaded by the medium, is investigated. The efficiency of energy fluxes is shown, since not only the kinematic and dynamic characteristics of the vibration field are taken into account, but also the phase shift between them. This allows predicting dangerous modes of vibrations of shells and shell-media systems in their design. [⤤], [⤤], [⤤]

• The effect of negative group velocity for "dry" shells of Kirchhoff–Love type was found. This effect was investigated both for "dry" shells and for shells loaded with liquid or Winkler base. Asymptotic estimates of the frequency ranges and wave numbers where the negative group velocity effect is observed are obtained, as well as estimates of the maximum negative group velocity in the system. These results can be useful for predicting the occurrence of dangerous modes of operation of pipelines and other similar systems. [⤤], [⤤], [⤤], [⤤]

• The effect of factorization of the equations of passband and stopband boundaries in infinite periodic shells is found. Explicit expressions of factorization of these equations in the case of rods and beams loaded with periodic masses have been obtained. Energy flows and vibration fields in such systems are investigated. [⤤], [⤤], [⤤]

• Formulas linking the frequency shift caused by hydrogen embrittlement of the shell with the parameters of the shell, the attenuation coefficients and the degree of wear with time were obtained. This, in turn, makes it possible to predict the frequency shift and, thus, to avoid the undesirable shell oscillations dangerous for its strength. [⤤], [⤤]

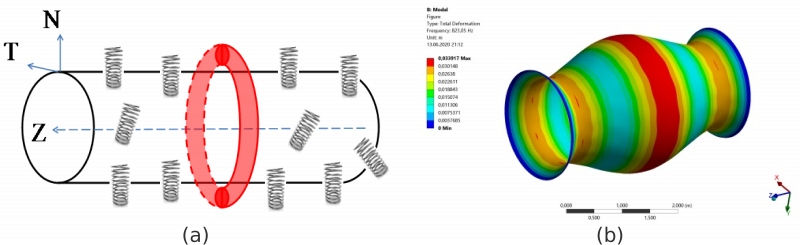
Oscillations of the cylindrical shell on Winkler base loaded with a mass belt: (a) physical model, (b) visualization of displacements.